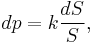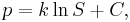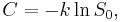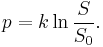Weber–Fechner law

The Weber–Fechner law is a confusing term, because it combines two different laws. Some authors use the term to mean Weber's law, and others Fechner's law. Fechner himself added confusion to the literature by calling his own law Weber's law.[1] Ernst Heinrich Weber (1795–1878) was one of the first people to approach the study of the human response to a physical stimulus in a quantitative fashion.[2] His law states that the just-noticeable difference between two stimuli is proportional to the magnitude of the stimuli. Gustav Theodor Fechner (1801–1887) later offered an elaborate theoretical interpretation of Weber's findings, in which he attempted to describe the relationship between the physical magnitudes of stimuli and the perceived intensity of the stimuli. Fechner's law states that subjective sensation is proportional to the logarithm of the stimulus intensity.

Contents

Derivation of Fechner's law for weight perception

Weber found that the just noticeable difference (jnd) between two weights was approximately proportional to the mass of the weights. Thus, if 105 g can (only just) be distinguished from 100 g, the jnd (or differential threshold) is 5 g. If the mass is doubled, the differential threshold also doubles to 10 g, so that 210 g can be distinguished from 200 g. This kind of relationship can be described by a differential equation as,

dp = k\frac{dS}{S} , \,\!

where dp is the differential change in perception, dS is the differential increase in the stimulus and S is the stimulus at the instant. A constant factor k is to be determined experimentally.

Integrating the above equation gives

p = k \ln{S} %2B C, \,\!

where C is the constant of integration, ln is the natural logarithm.

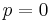To determine C, put p = 0, i.e. no perception; then subtract 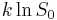k\ln{S_0} from both sides and rearrange:

C = -k\ln{S_0}, \,\!

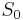where S_0 is that threshold of stimulus below which it is not perceived at all.

Substituting this value in for C above and rearranging, our equation becomes:

p = k \ln{\frac{S}{S_0}}. \,\!

The relationship between stimulus and perception is logarithmic. This logarithmic relationship means that if a stimulus varies as a geometric progression (i.e. multiplied by a fixed factor), the corresponding perception is altered in an arithmetic progression (i.e. in additive constant amounts). For example, if a stimulus is tripled in strength (i.e., 3 x 1), the corresponding perception may be two times as strong as its original value (i.e., 1 + 1). If the stimulus is again tripled in strength (i.e., 3 x 3 x 1), the corresponding perception will be three times as strong as its original value (i.e., 1 + 1 + 1). Hence, for multiplications in stimulus strength, the strength of perception only adds. The mathematical derivations of the torques on a simple beam balance produce a description that is strictly compatible with Weber's law (see link1 or link2).

Fechner did not conduct any experiments on how perceived heaviness increased with the mass of the stimulus. Instead, he assumed that all jnds are subjectively equal, and argued mathematically that this would produce a logarithmic relation between the stimulus intensity and the sensation. These assumptions have both been questioned.[3][4] Most researchers nowadays accept that a power law is a more realistic relationship, or that a logarithmic function is just one of a family of possible functions.[5]

Other sense modalities provide only mixed support for either Weber's law or Fechner's law.

The case of vision

The eye senses brightness approximately logarithmically over a moderate range (but more like a power law over a wider range), and stellar magnitude is measured on a logarithmic scale.[6] This magnitude scale was invented by the ancient Greek astronomer Hipparchus in about 150 B.C. He ranked the stars he could see in terms of their brightness, with 1 representing the brightest down to 6 representing the faintest, though now the scale has been extended beyond these limits; an increase in 5 magnitudes corresponds to a decrease in brightness by a factor of 100.[6] Modern researchers have attempted to incorporate such perceptual effects into mathematical models of vision.[7][8]

The case of sound

Weber's law does not quite hold for loudness. It is a fair approximation for higher intensities, but not for lower amplitudes. Similarly, the law applies loosely to pitch perception. The mel scale is a proposed perceptual scale of pitch that maps sound frequency change to perceived pitch change. Below 500 Hz, this mapping is near linear, but above 500Hz, the relationship is approximately logarithmic.[9]

The Weber–Fechner law holds approximately for musical tempo (the difference between a tempo of 60 beats per minute and 61 bpm is perceived as a much larger difference than between 200bpm and 201bpm).[10]

"Near miss" of Weber's law in the auditory system

Weber's law does not hold at perception of higher intensities. Intensity discrimination improves at higher intensities. The first demonstration of the phenomena were presented by Riesz in 1928, in the Journal of Acoustical Society of America. This deviation of the Weber's law is known as the "near miss" of the Weber's law. This term was coined by McGill and Goldberg in their paper of 1968 in the Journal of Acoustical Society of America (JASA). Their study consisted of intensity discrimination in pure tones. Further studies have shown that the near miss is observed in noise stimuli as well. Jesteadt et al. in their 1976 paper demonstrated that the near miss holds across all the frequencies, and that the intensity discrimination is not a function of frequency, and that the change in discrimination with level can be represented by a single function across all frequencies.

The case of numerical cognition

Psychological studies show that numbers are thought of as existing along a mental number line.[11] Larger entries are on the right and smaller entries on the left. It becomes increasingly difficult to discriminate among two places on a number line as the distance between the two places decreases—known as the distance effect.[12] This is important in areas of magnitude estimation, such as dealing with large scales and estimating distances. See this article [1] on logarithmic number representation.

See also

References

  1. ^ Reber, A.S.(1985) The Penguin dictionary of psychology. London: Penguin Books
  2. ^ Ross, H.E. and Murray, D. J.(1996)(Ed. and Transl.) E.H.Weber on the tactile senses. 2nd ed. Hove: Erlbaum (UK) Taylor & Francis.
  3. ^ Heidelberger, M. (2004)Nature from within: Gustav Theodor Fechner and his psychophysical worldview. Transl. C. Klohr. Pittsburgh, USA: University of Pittsburg Press.
  4. ^ Masin, S.C., Zudini, V. and Antonelli, M. (2009) Early alternative derivations of Fechner's law. pdf J. History of the Behavioral Sciences, 45: 56–65.
  5. ^ Murray, D.J. (1993) A perspective for viewing the history of psychophysics. Behavioral and Brain Sciences, 16: 115–186.
  6. ^ a b V. B. Bhatia (2001). Astronomy and astrophysics with elements of cosmology. CRC Press. p. 20. ISBN 9780849310133. http://books.google.com/books?id=k4XRQpKV9kgC&pg=PA20. 
  7. ^ Jianhong (Jackie) Shen; Yoon-Mo Jung (2006). "Weberized Mumford–Shah model with Bose–Einstein photon noise". Appl. Math. Optim. 53 (3): 331–358. doi:10.1007/s00245-005-0850-1. http://www.springerlink.com/content/172467181w543245/?p=cab484b467b64e729a4666703e273f95&pi=3. 
  8. ^ Jianhong (Jackie) Shen (2003). "On the foundations of vision modeling I. Weber's law and Weberized TV (total variation) restoration". Physica D: Nonlinear Phenomena 175 (3/4): 241–251. doi:10.1016/S0167-2789(02)00734-0. 
  9. ^ Moore, B. C. J., Tyler, L. K., and Marslen-Wilsen, W. D. (2009). The perception of speech: From sound to meaning. Oxford University Press: Oxford.
  10. ^ Scheirer E.D. (January 1998). "Tempo and beat analysis of acoustic musical signals" (PDF). J. Acoust. Soc. Am. 103 (1): 588–601. http://www.iro.umontreal.ca/~pift6080/H09/documents/papers/scheirer_jasa.pdf.  See p. 595, bottom
  11. ^ Moyer R.S., Landauer T.K. (September 1967). "Time required for judgements of numerical inequality". Nature 215 (5109): 1519–20. doi:10.1038/2151519a0. PMID 6052760. 
  12. ^ Longo M.R., Lourenco S.F. (2007). "Spatial attention and the mental number line: evidence for characteristic biases and compression". Neuropsychologia 45: 1400–6. doi:10.1016/j.neuropsychologia.2006.11.002. http://www.sciencedirect.com/science?_ob=ArticleURL&_udi=B6T0D-4MHPC4G-1&_user=201547&_rdoc=1&_fmt=&_orig=search&_sort=d&view=c&_acct=C000014058&_version=1&_urlVersion=0&_userid=201547&md5=ed6a3e2bc764c04edd25cc50f703b49e. 

External links